センター試験における「地学基礎」の特徴
大学への入学を目指す生徒のみなさんにとって、センター試験は大学入試における最初の入口だといえるでしょう。
私自身、これまで高等学校の地学の問題を作成したり、センター試験の地学基礎において高得点を取る方法を指導してきたりしました。
本ページでは、地学基礎を勉強されるみなさんに向けて、まずは私の経験から導き出された地学という科目の問題の捉え方についてお伝えしていきます。
試験問題では嘘を出すことができない
センター試験に限らず、そもそも大学入試における試験問題というものには、嘘や間違ったデータ・情報を出すことができません。
特に、センター試験というものは大学入試における共通の一次試験という位置づけであり全国の高校生が受験するものですので、作問者の威信にかけて問題の作成が行われるという特徴があります。
そのため、センター試験においては掲載される問題の中に嘘の情報や間違ったデータがあってはならないという部分に対して非常に敏感なところがあります。
さて、地学という科目は、まだまだ知られていない自然現象や観測されていない出来事というものがたくさん存在している中から、「これは絶対に間違いがない部分」が取り出されて構成されているという特徴があります。
ですので、地学の教科書あるいは試験問題に出てくる数値や出来事は、すべて間違いのない「事実」として取り扱われる必要があるわけです。
たとえば、地学では知識を問うような問題よりも計算問題が数多く出てきますが、実際にフィールドに出て観測される数値データというものにはどうしても誤差や数値のばらつきというものが出てきてしまいます。
実際に地学の問題を作成する人間からすると、このような定まっていない数値をそのまま使って計算問題などを作成してしまうと、きれいな数値として解答が出せなくなることになってしまいます。
特に、地学における計算にはさまざまな要素を用いて複雑になることが多いために、解答としてきれいな出しやすいような数値にするためには、端数を削ったり「●●の数値を使って計算せよ」という前提となる数値を用意したりすることになります。
つまり、地学の試験問題で使われる数値データや取り扱われる用語・出来事は、ある程度定まってしまうことにつながっていくわけです。
そのため、それらの数値をあらかじめ覚えておけば、数値を見ただけで地学のどのあたりの分野の問題か、何が問われそうか、さらには答えが何かというところまで一瞬で分かってしまうということも出てきます。
特に、センター試験では問題を解くための時間は限られていますので、地学基礎の問題に取り組む際には、典型的な問題を押さえておき、そこで出てきた数値やデータについては覚えてしまうことが高得点を取るための秘訣になってくるわけです。
以上のことから、地学の試験で高得点を目指すためには、そこで問われるデータや数値を問題演習のときに一緒に覚えておくことがかなり有効な戦術になるといえるのです。
地学の問題の特徴
ただし、地学の問題に取り組む際にはこのような数値やデータを暗記すること以上に、出題される問題をどのように捉えるのかという部分がもっとも大切になってきます。
ここで、実際の問題を見ながらこのことについて考えてみましょう。
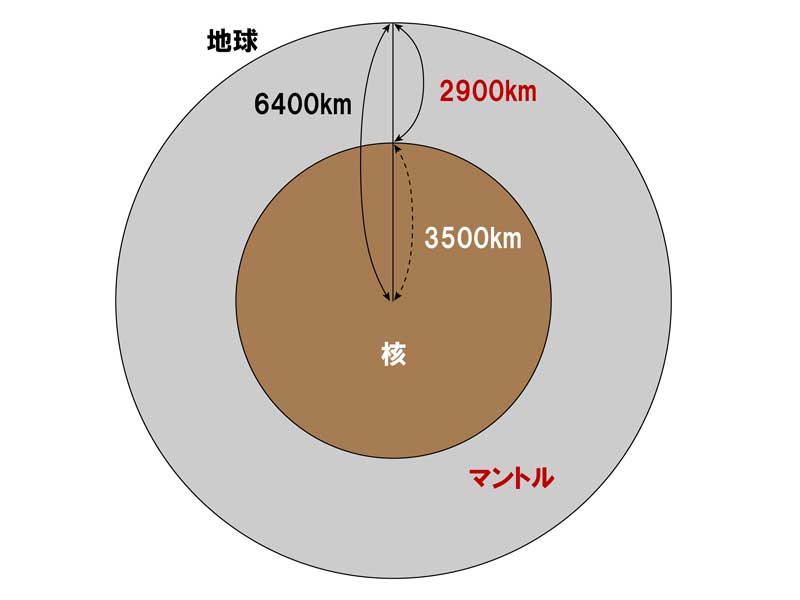
(問) 地球の核の平均密度に関する次の問いに答えよ。
地球の核の体積は、地球全体の体積の約6分の1である。
地球の平均密度を5.5(g/cm3)、地殻を含めたマントルの平均密度を4.0(g/cm3)とすると、地球の核の平均密度ρ(g/cm3)はいくらになるか。計算によりその値を求めよ。
ただし、地球は半径6400(km)の球であり、地表からマントルと核の境界までの距離を2900(km)とする。またρの値は小数点以下第1位まで示しておくこと。
以上の問題に対して、みなさんはどのような解答の方針を立てるでしょうか。
まず、この問題では地球の核の密度を求めますので、密度を求める公式として「密度=質量 / 体積」を使う必要があり、密度をρ(ロー)、質量をMとして体積をVとおくと、「密度(ρ)=質量(M)/体積(V)」という文字式が成り立ちます。
次に、球体の体積(V)の公式は「4/3πr3」で、この「r」は球体の半径ですのでその数値を代入すれば体積(V)が算出できます。
また、質量(M)はどのように算出するかというと、これは体積(V)に密度(ρ)を掛け合わせることで求められますので、「質量(M)=体積(V)×密度(ρ)」になります(この式そのものは先ほどの密度(ρ)の式を変形したものです)。
さて、核の密度(ρcとします)を出すためには、「核の質量(Mc)/核の体積(Vc)」となりますので、その質量(Mc)と体積(Vc)をそれぞれ求める必要があります。
核の質量(Mc)は、地球の質量(Me)からマントルの質量(Mm)を引くことで求められますので、「Mc=Me-Mm」となります。
ただし、ここの最後のマントルの質量(Mm)は、地球の体積(Ve)から核の体積(Vc)を引き算した結果にマントルの密度(ρm)をかけあわせることで算出する必要があるので、「Mm=(Ve-Vc)×ρm」という計算になります。
核の体積(Vc)は、「4/3πr3」の「r」に核の半径、すなわち地球の半径6400(km)からマントルの半径2900(km)を引き算した3500(km)を代入することで求められます。
以上のことをすべて式で表現すると、以下のようなことになってきます。
核の密度(ρc)を求めるためには上式を計算して解くこと必要があるのですが、ここでさらに密度の単位には「cm」が用いられていますので、kmの数値をcmに変換し、より大きな数字を使って計算することが加わってくるのです。
ここまで見てきただけでも分かるとおり、限りある試験時間の中でこのような大変な計算をすることは現実的な問題としてはかなり厳しいといえるでしょう。
もちろん、この計算をやってやれないことはありませんが、もともと地学では扱う対象が大きいことからその数値が大きくなりやすく、また単位を揃えるための変換計算が入ってくることも多いため、やはり解答へ近づくための筋道の立て方が他にあるのではないかと考えることが地学の問題を考える際には順当な方向性になるわけです。
地学的な問題の捉え方
では、地学教師である私ならば以上の問題をどのように考えるのかというと、問題の最初の前提に挙げられている「地球の核の体積は地球全体の体積の1/6である」という部分に注目します。
問題文の前提として数値や条件を指定しているということは、暗にそれをどこかで用いるということを示していることのあらわれだといえます。
核の体積が地球全体の体積の1/6ということは、核をのぞいた地殻とマントルの体積は残りの5/6となるはずです。
このように単純に考えると、以下のような解答の方針を立てることができます。
以上の考え方をして文字式への置き換えを行うと、計算が非常に単純なものとなります。
なお、この核の平均密度の「13.0g/cm3」はよく出てくる数値ですので、これに限らず地学では覚えておけばいろいろと役に立ちます。
特に、センター試験の問題は選択肢で解答するものですので、もし、私のように核の平均密度の数値を覚えている人ならば「13~15の範囲に解答の数値がある」という解答に対するあたりをつけることができるようになりますし、そうなると計算そのものをせずに正解の選択肢が選べるということになるのです。
以上のように、センター対策として地学基礎を勉強されるみなさんには、地学の問題の「捉え方」や「考え方」というものに特に慣れ親しんでもらうことを大切にしてもらえればと思います。


