地球の形――実は丸くはありません
太陽系の歴史を押さえたところで、次はいよいよ私たちの住んでいる地球のことについて学んでいきましょう。
地球は丸い形、より正確には球体の形をしていることについては、みなさんすでにご存知でしょう。
ただし、一般的にはそのように言われているものの、地学的に見ればこの表現は正しくありません。
今回は、地学の観点から見た地球の形について考えていきましょう。
人類はいつ地球の形が丸いことに気づいたか
私たちは「地球が丸い形をしている」ということを知識としては知っていますが、普段生活していても地面はどこまで行っても平らなように感じられますので、それを実感することはほとんどないと言っていいでしょう。
地球の形が丸い形をしているらしいことに最初に気づいたのは、古代ギリシャの哲学者アリストテレスだと言われています。
では、彼はどのようなことをきっかけとして地球の形に気づくことができたのでしょうか。
まず、太陽や月が丸い形をしていることから自分たちの地球も丸い形をしているのではないかと類推したことが挙げられます。
次に、月食の際に月に映っている丸い形の影が地球の影をあらわしているのではないかと考えたことが知られています。
また、港を出発した船が水平線に近づいていくと、船のマストが下方向に徐々に短くなりやがて見えなくなっていき、反対に船が水平線から港に近づいてくる際にはその逆になるという現象が観察されたことです。
この現象を説明するためには、水平線の向こう側が下の方向に対して落ち込んでいる、すなわち地球が丸い形をしている必要があるとアリストテレスは考えたわけです。
回転する楕円体としての地球
さて、このようにして人類は地球の形が丸いということを知ったわけですが、それは地球儀のような美しい球体の形をしているわけではありません。
地学では、これまで地球の実際の形をできるだけ正確に表現するためにいろいろな形状の地球が考えられてきました。
その代表的なものが、地球は完全な球体ではなく回転する楕円体、すなわち「回転楕円体」とよばれる形です。
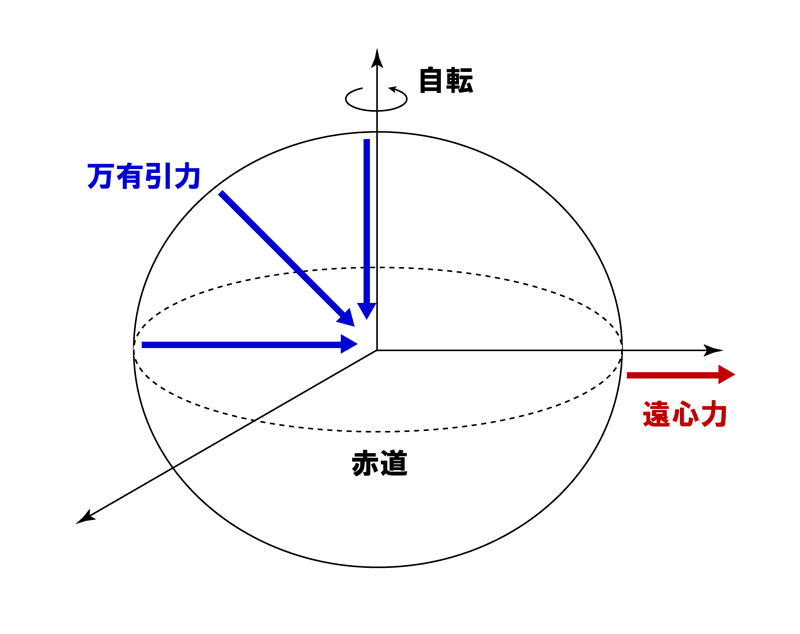
これはニュートンが提唱した考え方で、地球は自転しているために赤道に近づけば近づくほど自転による遠心力のはたらきが強くなり、円形が少し横長になった楕円体の形になるというものです。
以下の表は南北の子午線上の緯度(天文緯度)の1度あたりの距離を実際に比較した数値で、緯度差が同じ1度でも極付近での距離が長いのに対して赤道に近づけば近づくほど距離が短くなっているため、地球が楕円体の形になっていることが分かります。
| 場所 | 距離 |
|---|---|
| 北フィンランド | 約112km |
| フランス | 約111km |
| エクアドル | 約110km |
それで、地球の形をこのような回転楕円体として捉えることにどのような意味があるかですが、この考え方を取り入れることにより地球の場所によって重力のはたらき方に違いがあることが説明できるようになるのです。
たとえば、同じ1kgの物体であっても北極点や南極点における重力と赤道付近における重力には違いがあり、赤道付近の方がその値が小さくなることが分かっています(以下の表参照)。
| 緯度 | 1kgの物体にはたらく重力の大きさ(N) |
|---|---|
| 90度 (北極・南極) |
9.832 |
| 60度 | 9.819 |
| 30度 | 9.793 |
| 0度 (赤道) |
9.780 |
もし、地球が完全な球形だとするとなぜこのような重力の違いが出てくるのかについて説明することができないのです。
そこで地球の形状を回転楕円体として考えることで、次の2つのことからこれらの重力の違いを説明することができます。
まず、極付近から地球の中心までの距離と赤道から地球の中心までの距離を比較した場合、前者に比べて後者の方が距離が長くなり、その分だけ中心への重力が弱くなること。
次に、赤道付近では極付近に比べて遠心力が加わるために、重力のはたらきが弱くなること。
これら2つの仮説により、地球における重力の違いを説明することができるようになったのです。
太陽系における惑星の形状の違い
いずれにせよ、地球を回転楕円体として捉えることで地球上の重力や引力に関係するさまざまな現象が説明ができるようになりました。
ちなみに、地球の中心から北極(あるいは南極)までの距離はおおよそ6357km、地球の中心から赤道までの距離はおおよそ6378kmという長さの違いがあります。
それで、この2つの数値を使って地球がどの程度の楕円形をしているのかについて、「扁平率」(へんぺいりつ)という割合を算出することができます。
扁平率は、以下のような式で表現されます
この式に先程のそれぞれの半径の数値を代入すると、地球の扁平率はおおよそ1/298という結果が出てきますが、これはとても小さい値なので地球はほとんど球体に近い楕円体だということが分かります。
それでは最後に、太陽系の他の惑星は地球と比べてどのような形状の違いがあるのかを比較してみましょう。
地球以外の惑星も丸い形をしていますが、そこには若干の違いがあります。
まず、金星は地球に比べてより球体に近い惑星として知られています。
その理由としては、自転の周期が243日と非常に長い、すなわち自転の速度が非常に遅いために結果的に回転楕円体としての扁平率の値が極端に小さくなることが挙げられます。
逆に、木星や土星は地球よりも扁平率の値が大きい、すなわちより平べったい形状の惑星となっています。
その理由は金星とはまったく逆で、どちらも自転の周期がとても短い(土星が9.8時間、木星が10.2時間でそれぞれ一周する)、すなわち自転の速度が速いためにより強い遠心力がはたらき、扁平な形状になってしまうというわけです。